Real Roots –> Unimodal Coefficients

A polynomial in one variable $x$ is a combination of powers of $x$ . For example, $p(x) = x+1$ or $q(x) = x^2+4x+1$ are polynomials, while $f(x) = x^2-2^x$ is not a polynomial, since the term $2^x$ cannot be written as powers of $x$ (at least as a finite combination of such powers).

A root of a polynomial $p(x)$ is a number $c$ for which $p(c)=0$ . With the polynomial $p(x)=x+1$ above, $c=-1$ is a root since $p(-1)=-1+1=0$ . When the highest power of $x$ in a polynomial (called the degree of the polynomial) is $2$ , we all the polynomial a quadric (in the literature it seems that quadric is used as a noun while quadratic is used as an adjective). You may recall the quadratic formula that produces the roots of such polynomials: for a quadratic

$q(x) = ax^2+bx+c$ ,

the roots are

$x=\frac{-1}{2a} \left( b\pm \sqrt{b^2-4ac} \right)$ .

Let’s consider two quadratic polynomials $q(x) = 2x^2+x+2$ and $p(x) = x^2+4x+1$ . Using the quadratic formula, the roots of $q(x)$ are

$x = \frac{-1}{4} \left(1\pm \sqrt{-15} \right)$

and the roots of $p(x)$ are

$x = \frac{-1}{2} \left(4 \pm \sqrt{12} \right) \approx -3.732, -0.27$ .

I did not approximate the roots of $q(x)$ , because they are not real numbers. The $\sqrt{-15}$ is not a real number; it is called a complex or imaginary number. To see that it is not real, let’s suppose it is and see what happens.

Let’s say $\sqrt{-15}=a$ for some real number $a$ . Then squaring both sides, we get $-15=a^2$ . If you square a positive number, the result is positive. If you square a negative number, the result is also positive. Yet we have $a^2 <0$ , so we have arrived at a contradiction. Therefore, $\sqrt{-15}$ cannot be a real number.

We can see this on the graphs of the two functions:

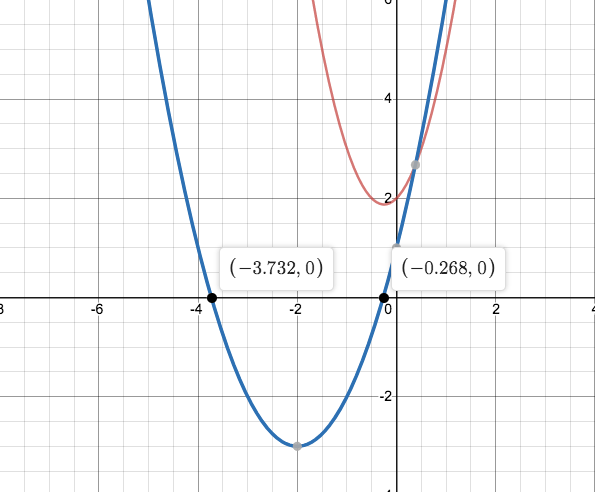
The red graph is $q(x)$ and the blue graph is $p(x)$ . We see that the blue graph crosses the $x$ -axis exactly at the roots we found, and that the red graph never touches the $x$ -axis. When a root does cross the $x$ -axis, or, equivalently, is not complex, we say it is a real root. The rest of the post focuses on real roots.

One of the oldest problems in mathematics is how to find roots of polynomials. Indeed, there used to be competitions with big monetary prizes for who could compute roots the fastest, and if you found a general formula for the roots (like the quadratic formula), you became famous in the math world. There are actually formulas when the degree is $1,2,3$ , or $4$ , and there are incredibly wonderful proofs from different branches of mathematics that show that no formula for degree $5$ can exist.

What I now describe is not a method to find real roots, but rather a condition which says when real roots do not exist. Let’s look at two more polynomials with their graphs.

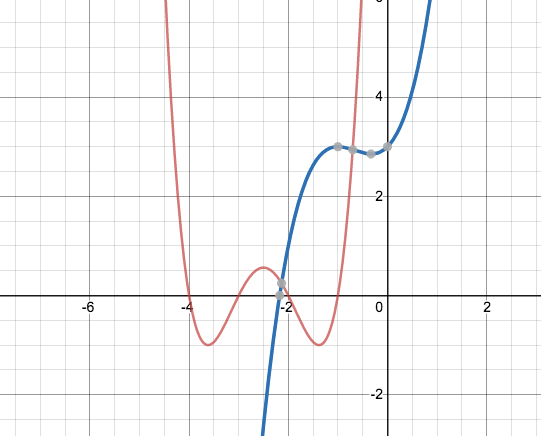
The red graph is the graph of

$p(x) = x^4+10x^3+35x^2+50x+24$

and the blue graph is the graph of

$q(x) = x^3+2x^2+x+3$

The numbers in front of each power of $x$ are called coefficients. The sequence of coefficients of $p(x)$ are $(1,10,35,50,24)$ , the the sequence of coefficients of $q(x)$ are $(1,2,1,3)$ .

Notice that the red graph crosses the $x$ -axis four times, and the blue graph only crosses the $x$ -axis once. The degree of $p(x)$ is $4$ , and the degree of $q(x)$ is $3$ . It is not hard to show (or see) that a polynomial of degree $d$ cannot have more than $d$ roots. Therefore, all roots of $p(x)$ are real, and there are some non-real roots of $q(x)$ (the blue graph crosses the $x$ -axis like a straight line, which means the roots has multiplicity one, which I won’t go through the trouble of defining – but this is why the latter statement is true).

Now here is the fascinating fact: I could have told you that $q(x)$ had some non-real roots within 2 seconds of looking at the equation! This fact follows solely from the coefficients of $q(x)$ . Think of the sequence of coefficients by comparing neighbors:

$1 < 2 > 1 < 3$

There are too many inequality switches for this polynomial to have all real roots. Earlier we saw that the quadric $2x^2+x+2$ had non-real roots too, and notice that

$2 > 1 < 2$ .

Compare this to the sequences of coefficients of $p(x)$ :

$1 < 10 < 35 < 50 > 24$ .

This is an example of a unimodal sequence of numbers; more generally, a unimodal sequence of numbers increases up to a peak (in this case, $50$ ), and if the sequence begins to fall, it never rises again.

We can now state the Main Theorem:

Theorem: If the sequence of coefficients of a polynomial is not unimodal, the the polynomial has non-real roots. Said differently, if all the roots of a polynomial are real, then the sequence of coefficients is a unimodal sequence.

The rest of this post gets pretty formal.

Before we start, let’s define one more thing: the derivative. This term is essential in calculus, and instead of going in depth, I’ll just say what it is for a polynomial: the derivative of a polynomial $p(x)$ is computed term-wise by taking $cx^n$ and turning it into $nc x^{n-1}$ . We write $D'p(x)$ for the final result. For example, for

$p(x) = x^4 + 10x^3 + 35x^2 + 50x +24$

we get

$D'p(x) = 4x^3 + 30x^2 + 70x + 50$ .

If we did this again, we would call it $D^2 p(x)$ , and so on. You can easily check that $D^4 p(x)=4\times 3\times 2\times 1 = 24$ , and $D^n p(x)=0$ for $n\geq 5$ .

The Main Theorem with Proof

First we formalize a term mentioned above and then re-state the Main Theorem. Let $a_0,\dots, a_n$ be a sequence of positive integers. If there is some $j$ for which

$a_0\leq \dots \leq a_{j-1} \leq a_j \geq a_{j+1} \geq \dots \geq a_n,$

then we say that the sequence is unimodal.

Theorem: Let $a_0,\dots, a_n$ be a sequence of positive integers. If all roots of the polynomial

$p(x)=a_0 + a_1x+\dots +a_nx^n$

are real, then $a_0,\dots, a_n$ is a unimodal sequence.

This theorem is proven by the following three steps.

Proposition 1: If all roots of

$p(x) = \sum_{k=0}^n {n \choose k} a_k x^k$

are real, then $a_j^2 \geq a_{j-1}a_{j+1}$ for all $j$ .

Corollary 2: If all roots of

$p(x) = \sum_{k=0}^n a_k x^k$

are real, then $a_j^2 \geq a_{j-1}a_{j+1}$ for all $j$ .

Lemma 3: If $a_0,\dots, a_n$ are positive integers and $a_j^2 \geq a_{j-1}a_{j+1}$ for all $j$ , then the sequence is unimodal.

Proof of Lemma 3: Suppose $a_0\leq a_1\leq \dots \leq a_j \geq a_{j+1}$ . We need to show that $a_{j+1}\geq \dots \geq a_n$ . To show $a_{j+1}\geq a_{j+2}$ , since these are positive, it suffices to show $a_j a_{j+1} \geq a_j a_{j+2}$ . But $a_j \geq a_{j+1}$ , so

$a_j a_{j+1} > a_{j+1}^2 \geq a_j a_{j+2}$ .

Applying this argument inductively, we obtain the result. $\blacksquare$

Proof of Corollary 2: As the name suggests, this proof depends on Proposition 1, which we are proving next. Assuming its truth, we define a new sequence $b_0,\dots, b_n$ by setting

$b_k = a_k / {n \choose k}$ .

Then

$p(x) = \sum_{k=0}^n {n \choose k} b_k x^k$

has all real roots, so $b_j^2 \geq b_{j-1}b_{j+1}$ for all $j$ by Proposition 1. It is easily checked that this implies $a_j^2 \geq a_{j-1}a_{j+1}$ for all $j$ . $\blacksquare$